原文链接 http://www.lelovepan.cn/2015/11/25/%E5%8F%B0%E5%A4%A7%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E5%9F%BA%E7%9F%B3%E7%AC%94%E8%AE%B04-2.html
注:以下为加速网络访问所做的原文缓存,经过重新格式化,可能存在格式方面的问题,或偶有遗漏信息,请以原文为准。
补救措施(使机器学习成为可能)
我们通过上一节课,知道无法精确的通过已知样本来求得适合所有样本集的g。回想曾经学过的概率统计知识,即使我们不能够得到总体情况,但是依然可以通过抽样来“近似”得到总体大致的情况。
现在有一个很大的盒子,里面充满了很多很多的橘色和绿色的弹珠。

只要你学过概率与统计(即使没有学过,傻子也知道)就应该知道,我们完全可以试着来抽样嘛!
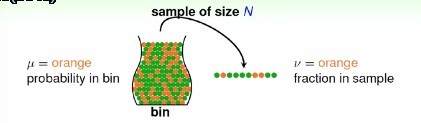
罐子(bin)里的橘色弹珠的比例为u,取样的橘色弹珠比例为v。他们两个的关系可以通过Hoeffding's Inequality来确定:

也就是说,u和v相差大于的概率为
我们很容易得出结论:当抽样样本很大或者能够容忍的估计误差Error=|u-v|较大时,完全可以由Hoeffding不等式来进行估计!