原文链接 https://morefreeze.github.io/2020/12/president-arbitrage.html
注:以下为加速网络访问所做的原文缓存,经过重新格式化,可能存在格式方面的问题,或偶有遗漏信息,请以原文为准。
{% include JB/setup %}
最近看了篇很有趣的文章,
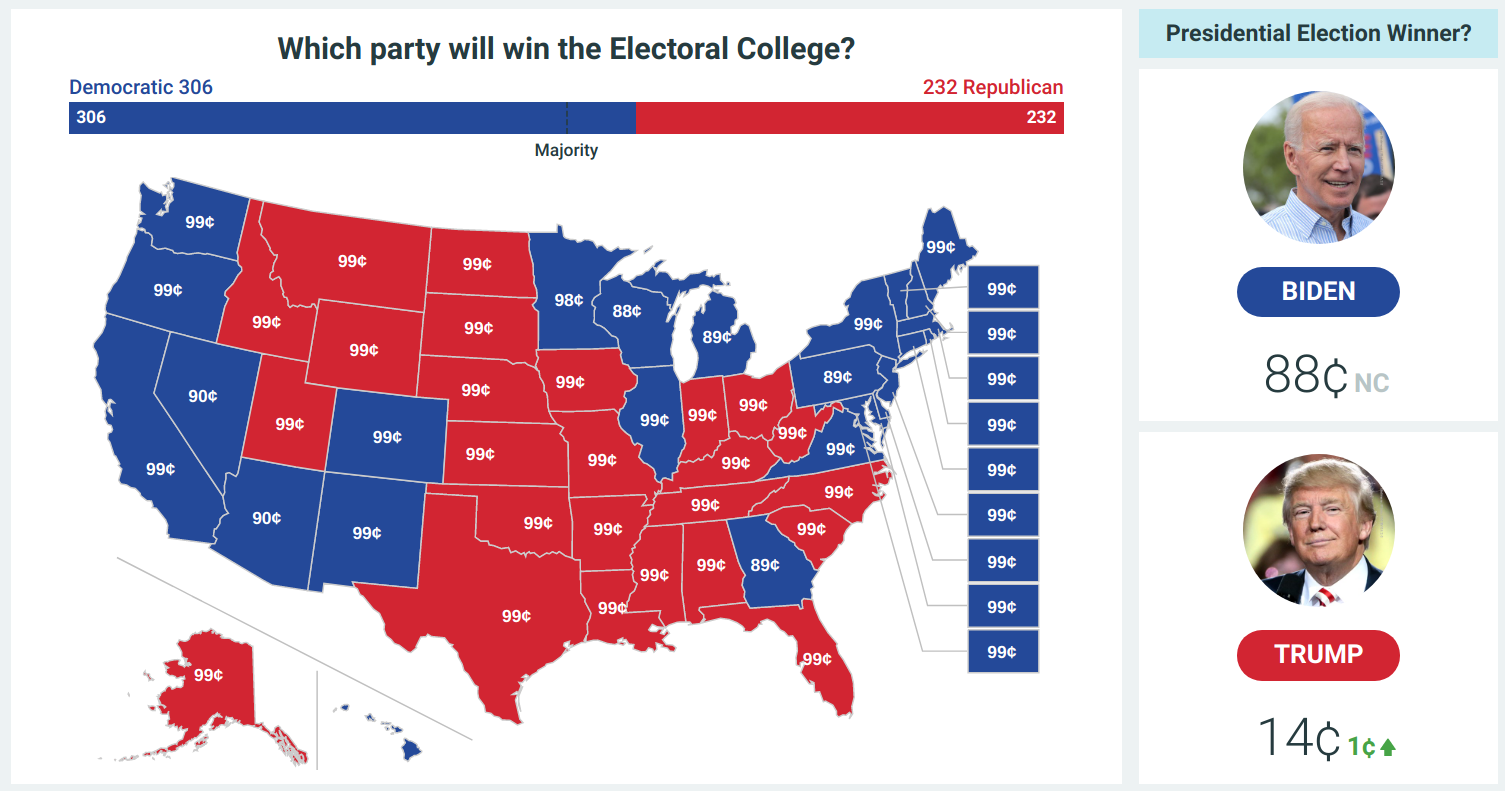
讲了有两个网站 A 和 B,都对 2020 年美国总统大选开了赌局,A 网站拜登胜出的赔率是 1:0.88,也就是说你可以花 0.88 买一注,
拜登胜出则你拿到 1 块,净赚 0.12,输则什么都没有亏掉那 0.88。B 网站允许你看空,看空拜登胜出(也就是认为拜登不会胜),
赔率就比较高了,是 1.05:0.05,就是你只要出 5 分钱(这里其实包含 1 分钱看空费,简化就不提了,感兴趣可以看原文),如果拜登没有当选,
那你拿到 1.05 净赚 1 块,输则损失掉 0.05。
 <!--more-->
<!--more-->
如何下注
如果按照赔率来计算概率的话,作者发现其实是有利可图的,A 网站相当于预测有 88% 的概率拜登会赢,而 B 网站则认为有 (1.05-0.05) / 1.05 = 95.2%拜登会赢(原文考虑看空费,实际是拿 1/1.04 算的,这里仍然简化),那就有 4.8%概率会输,88%+4.8% < 1 所以这里就存在套利的可能(为什么<1 就存在套利可能,后面也会证明)。
先给出拜登胜负在 AB 两个网站的损益表:
| 胜 | 负 | |
|---|---|---|
| A | +$0.12 | -$0.88 |
| B | -$0.05 | +$1.00 |
假设我们拿出 1 块投在 A 站,投入 B 站设为 X 元,为了使无论哪种结果都能有稳定的收入,使胜负收益相等,那么有$$1 / 0.88 0.12 - X = -0.88 + X / 0.05 1 \space [1]$$,解得$$X \approx 0.054$$,假设我们想获利 1000 元,即令等式一边等于 1000,设 N 为投入 A 站的钱数,有$$N*(0.12/0.88 - X)= 1000$$,解得$$N \approx 12157.89$$,由于每投入 1 块到 A 站,就有 X 元投入 B 站,实际投入 B 站$$N * X \approx657.89$$,与原文得出一致的结果。
凭什么能套利?
到这里细心的读者会发现上文的概率和等式并没有关系,那是不是用来判断是否能套利的呢?猜对了!接下来就来证明存在套利的条件是什么,而且也可以更简化上面 X 的计算过程。
一个错误的例子
首先,让我们随便试个场景,上面的 0.88,1.05 太难计算了,我们不妨假设 A 站赔率是 1.5:1,也即用一块可能净赚 0.5 元也可能亏掉这 1 块,B 站赔率是 2:1,同样,把这些值代入[1]中,有$$0.5/1 - X = -1 + X/1$$,解得$$X = \frac 3 4$$,但当你把 X 代入算的时候发现,等式是负值,这也就说明实际没有套利可能的,那么问题出在哪呢?
证明
让我们再形式化地定义下,假设 A 站的赔率是 A:1,B 站的赔率是 B:1(这里 B 站应该是 A 站事件相反的赔率),那么有$$(A-1) - X = -1 + (B-1)*X$$,化简得$$X = \frac A B$$,可把上面 A=1/0.88 和 B=1.05/0.05 代入验算,因为需要[1]式等号一边>0,因此有$$(A-1) - \frac A B > 0$$,因为 A>1,两边同时除以 A,得$$1 - (\frac 1 A + \frac 1 B)>0$$,而 1/A 和 1/B 正是概率,注意这里 A 站和 B 站事件应该互补,也即前面说的概率相加<1,即存在套利的可能。