使用numpy高效实现 k-means聚类

好久之前写过K-Means, 但写的极其丑陋，使用的时候还得用 sklearn.cluster.KMeans 包来干。最近需要手撕k-Means，自己也受不了多重for 循环这么disgusting的方式。sklearn.cluster.KMeans等包加入了相当多细节优化和向量化计算，同时也想能否用 numpy 来原生实现更高效的加速。在网上找了半天，终于看到简洁又高效的numpy 实现 了。

K-Means原理很简单。按照西瓜书的定义，就是在给定样本集 $D={x_{1},x_{2},...,x_{m}}$，找出簇中心$C={C_{1}, C_{2}...C{k}}$来最小化平方误差：

$ E=\sum_{i=1}^{k}\sum_{x\in{C_{i}}}\left|\right|\vec{x}-\vec{u_{i}}\left|\right|^2 $

说人话就是找到$k$ 个类中心，让所有样本被分在簇内的话样本相似度越高。但是这是个NP难问题，通常使用迭代优化来近似寻找$k$个类中心，也就是只要误差在可接受范围内就认为找到了所有样本到类中心的最小化误差。

这里我们首先随机或者基于某种策略生成$k$个簇中心，然后计算所有数据与 $k$ 个簇中心的距离，将数据根据与其相邻最近的簇中心分配为某个聚类，之后再次根据新的划分计算簇中心... 这样周而复始直到簇中心不再变化或者计算超出预期轮次，流程图如下：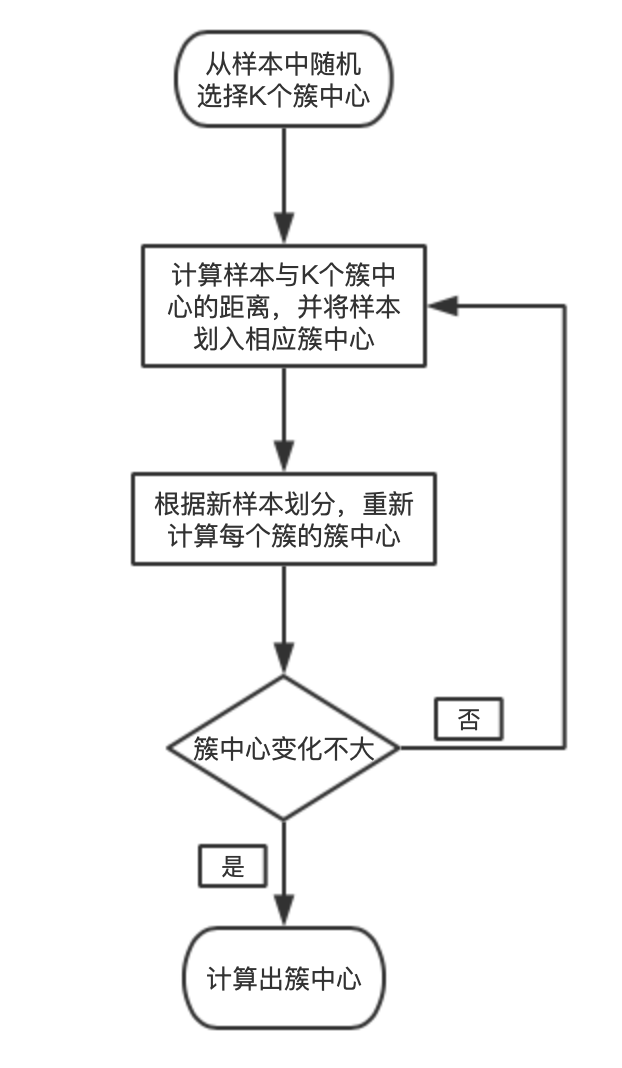

原理上较为简单，一般都可以简单实现。这里分析一下优化的点，计算所有样本与簇中心的时候，往往会使用 for循环 来遍历所有样本，并重新计算类中心。实际上 numpy 提供了广播机制(broadcasting)来进行高效矩阵计算，这在各个小型神经网络与计算图框架中均使用到了（MyGrad, micrograd, tinygrad），一直没有深入底层研究过。结合其他博主的文章来先看一看：https://zhuanlan.zhihu.com/p/60365398

这篇博客 就利用 *broadcasting *来进行的计算，实现上非常高效，我们对关键部分进行解析：

def kmeans(data, k=3, normalize=False, limit=500):
    # normalize 数据
    if normalize:
        stats = (data.mean(axis=0), data.std(axis=0))
        data = (data - stats[0]) / stats[1]

    # 直接将前K个数据当成簇中心
    centers = data[:k]

    for i in range(limit):
        # 首先利用广播机制计算每个样本到簇中心的距离，之后根据最小距离重新归类
        classifications = np.argmin(((data[:, :, None] - centers.T[None, :, :])**2).sum(axis=1), axis=1)
        # 对每个新的簇计算簇中心
        new_centers = np.array([data[classifications == j, :].mean(axis=0) for j in range(k)])

        # 簇中心不再移动的话，结束循环
        if (new_centers == centers).all():
            break
        else:
            centers = new_centers
    else:
        # 如果在for循环里正常结束，下面不会执行
        raise RuntimeError(f"Clustering algorithm did not complete within {limit} iterations")

    # 如果normalize了数据，簇中心会反向 scaled 到原来大小
    if normalize:
        centers = centers * stats[1] + stats[0]

    return classifications, centers

接下来就是产生一些随机数来测试一下吧

data = np.random.rand(200, 2)
classifications, centers = kmeans(data, k=5)

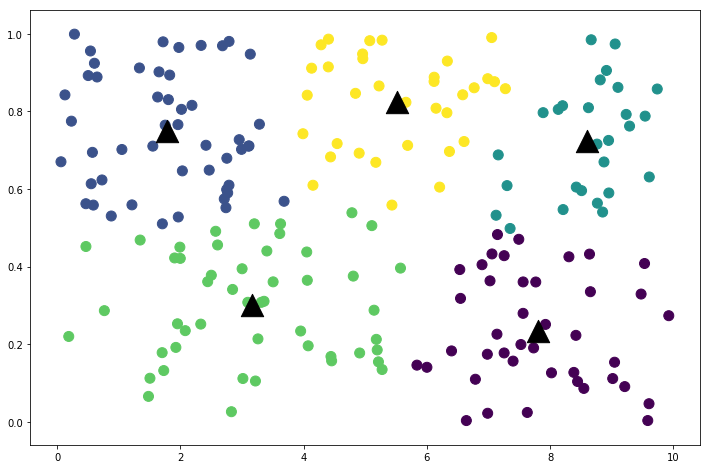
将聚类的结果可视化出来，每个类分别上不同的色，其中每个簇中心用黑色三角表示：

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

%matplotlib inline

plt.figure(figsize=(12, 8))
plt.scatter(x=data[:, 0], y=data[:, 1], s=100, c=classifications)
plt.scatter(x=centers[:, 0], y=centers[:, 1], s=500, c='k', marker='^');
# 16轮迭代结束

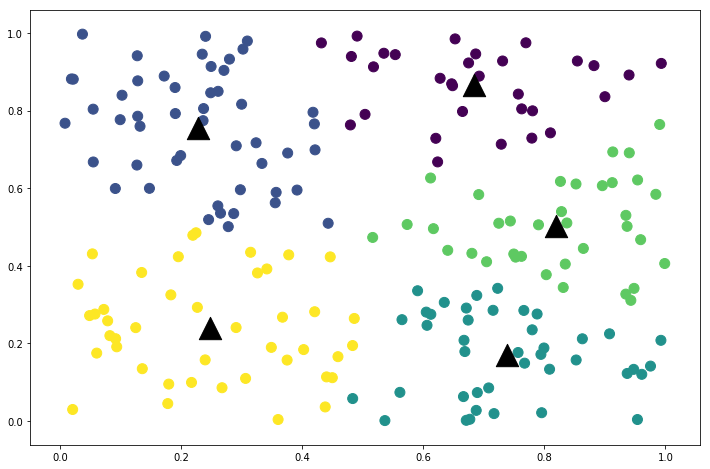
k-means算法对每个数据维数的相对尺度很敏感。如果某个维度是更大，距离函数会在该维度的计算权重会更大一些。直观一些，当我们将数据第一维扩大10倍后，观察一下：

data = np.random.rand(200, 2)
data[:, 0] *= 10  # 第一维扩大10倍

classifications, centers = kmeans(data, k=5)

plt.figure(figsize=(12, 8))
plt.scatter(x=data[:, 0], y=data[:, 1], s=100, c=classifications)
plt.scatter(x=centers[:, 0], y=centers[:, 1], s=500, c='k', marker='^');
# 13轮迭代结束

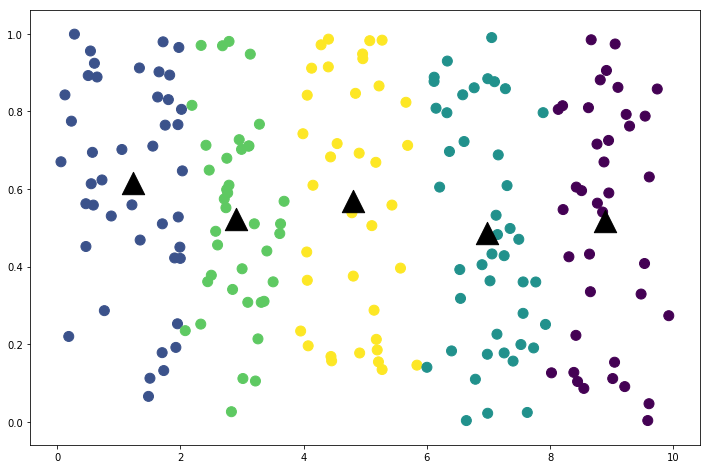
可以看到K-Means将数据在垂直方向分成了5类，很显然因为x轴的权重大于y轴（第1维度扩大了10倍）。使用归一化参数对数据进行归一化，可以得到更好的结果，我们可视化一下：

classifications, centers = kmeans(data, normalize=True, k=5)

plt.figure(figsize=(12, 8))
plt.scatter(x=data[:, 0], y=data[:, 1], s=100, c=classifications)
plt.scatter(x=centers[:, 0], y=centers[:, 1], s=500, c='k', marker='^');
# 9轮迭代结束

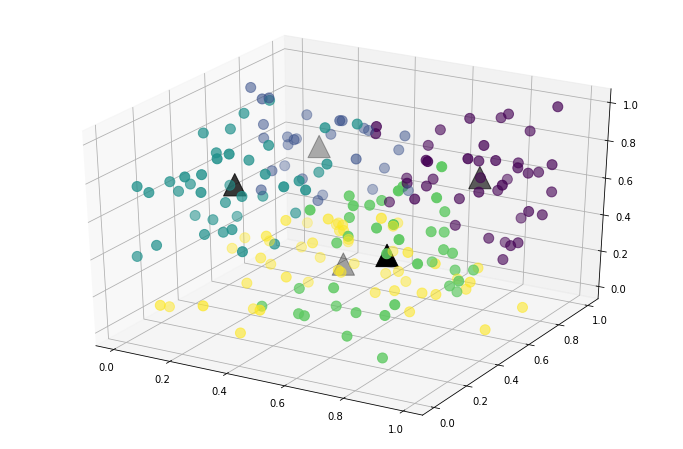
该算法还可以对2维以上数据进行聚类，下面进行3维聚类：

data = np.random.rand(200, 3)

classifications, centers = kmeans(data, normalize=True, k=5)

fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

ax.scatter(data[:, 0], data[:, 1], data[:, 2], c=classifications, s=100)
ax.scatter(centers[:, 0], centers[:, 1], centers[:, 2], s=500, c='k', marker='^');
# 8轮迭代