原文链接 https://drmingdrmer.github.io/tech/algorithm/2019/01/09/dict-cmp.html
注:以下为加速网络访问所做的原文缓存,经过重新格式化,可能存在格式方面的问题,或偶有遗漏信息,请以原文为准。
工作面试是个很有意思的过程, 面试经常是一个对未知领域初步了解的最好时机(对双方都是), 面试官和面试人通常也会尽力在最短的时间里表达/接受尽可能多的信息.
因此面试题一般也是比较有趣的: 它浓缩了日常工作中的典型和有挑战性的问题, 而又不会带有太多日常工作中的繁琐.
在技术面试中, 要哄好面试官, 最重要的无疑是能把一个问题解释的完善严谨.
于是打算收集一些 有趣 的问题, 跟大家分享. 本次先唠唠这个:
问题: 比较2个多级dict是否相同
2个多级dict可以看成2个树的对比, 此类问题应该在刷题网站上有不少了,
似乎用树的遍历就可以了, 然而可达鸭认为事情并不简单.
在深入答案之前, 我们先明确下问题的描述:
一个
dict中有多个key, 每个key对应一个子dict. 为了简化问题, 假设dict中的key对应的value都是dict, 没有其他类型.如果能够用来访问
a的所有的key也可以用来访问b, 就认为2个dict相同, 例如:a = {'foo':{'bar':{}}}; b = {'foo':{'bar':{}}}就是一对相同的dict:-
a['foo']和b['foo']都存在. -
a['foo']['bar']和b['foo']['bar']也都存在.
-
思路: 递归
比较2个dict同构的思路很直接:
对于2个
dict:a和b, 先比较这2个dict各自的key的集合一致, 如果不一致肯定2个dict不一样.再逐个对比每个key对应的子
dict是否一样. 直到遍历完所有的子dict.
def eq(a, b):
for k in set(a) | set(b):
if k not in a or k not in b:
return False
if not eq(a[k], b[k]):
return False
return True
print eq({}, {'x':{}}) # False
print eq({'x':{}}, {'x':{}}) # True
上面的代码差不多可以把大部分面试官哄到6成满意度.
但在实际使用中, 上面的代码还不太完善, 因为dict构成的图的节点之间可能存在
环形引用的情况, 如果有环, 上面的代码就会出现调用栈溢出.
所以在上面的代码基础上, 还需要加入有对环的处理.
几乎所有的语言对函数的递归调用层数都有限制, 例如python的限制是1000.
处理有环的情况
用python来举例描述2个有环的dict结构, 如下:
a = {}
b = {}
a['x'] = {} # a1
a['x']['x'] = a
b['x'] = {} # b1
b['x']['x'] = {} # b2
b['x']['x']['x'] = b
画出上面2个图的引用关系是酱的(其中a1, b1, b2等用来表示a, b中其他的子table):
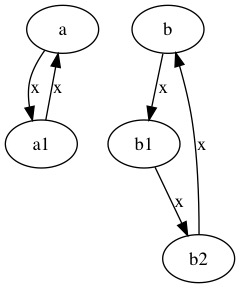
这里我们认为a和b是 访问相等 的:
因为对于访问者来说, 无法区分a和b的差别:
能用来访问a的路径, 也可以用来访问b, 反之也一样:
对于a和b来说:
a 和 b 都是合法的
a['x'] 和 b['x'] 都是合法的
a['x']['x'] 和 b['x']['x'] 都是合法的
a['x']['x']['x'] 和 b['x']['x']['x'] 都是合法的
在这个有环的例子中, 可以看出:
肯定存在一些公共路径是无限长的.
现在我们需要改进算法, 检查出环形的路径并及时终止递归遍历.
如果某个路径在
a中走到一个环上, 但在b中没有在一个环上, 就不用做特殊处理, 这种情况会自然的结束递归.需要处理的是一个路径p在
a,b上都对应到一个环的情况.
还是拿上面的各自成环的a, b为例, 对于一个无限长的公共路径p,
p = [x, x, x...], 它的每一步都通过key=x访问到下一个子dict.
这有, 它的每一步分别访问到的a, b上的 节点 如下
(a0和b0分别是a和b的根节点. a1, b2等是其他的节点:
a -> a0, b0 <- b
a['x'] -> a1, b1 <- b['x']
a['x']['x'] -> a0, b2 <- b['x']['x']
a['x']['x']['x'] -> a1, b0 <- b['x']['x']['x']
... -> a0, b1 <- ...
a1, b2
a0, b0
...
观察下上面的步骤可以发现, 最后路径p又会回到a0, b0的位置.
因为节点对的数量是有限的, 最多不超过 |a| * |b|个(|a|是a中的节点数),
那么如果一个路径p是无限长的,
那最终一定会在再次回到一个已经访问过的 节点对(上例中的a0, b0).
找到这个规律, 我们就有了剔除无限长路径的思路:
比较2个(可能有环型引用的)dict的算法:
遍历(广度优先/深度优先都可以), 枚举出所有查询路径p
对一个路径p, 检查它的一步
p[i]是否都能在a和b中走通, 如果不能, 则a和b存在一个不一致的路径, 失败退出.过滤出无限长的路径:
记录路径p在图
a,b中经过的 节点对, 如果p[i]访问到一个已经经过的 节点对, 则认为这个路径是环的, 不需要继续检查了, 回溯去检查其他路径.
python实现
def eq(a, b, walked=None):
walked = walked or {}
if (id(a), id(b)) in walked:
return True
walked[(id(a), id(b))] = True
for k in set(a) | set(b):
if k not in a or k not in b:
return False
if not eq(a[k], b[k], walked):
return False
return True
print eq({}, {'x':{}}) # False
print eq({'x': {}}, {'x':{}}) # True
a = {}
b = {}
a['x'] = a
b['x'] = {}
b['x']['x'] = b
print eq(a, b) # True
上面代码中, id() 用来取得一个对象的唯一id(原始类型的int, string等, 引用类型的dict,
list object都可以使用), 可以理解为c语言中的指针的角色.
效率分析
假设a, b的节点数分别是m和n,
那么, 因为整个遍历过程最多经一个 节点对 一次, 并且最多也需要记录所有的
节点对 的被访问的历史, 在上面的递归实现中,
最差情况是遇到一个经过了所有 节点对 的环, 因此:
时间效率:
O(n*m).空间效率:
O(n*m)(节点对记录的空间和递归调用栈的空间, 都是同样的级别).
更多
到此为止, 在这个问题上我希望我已经尽我所能把面试官哄好了.
如果还没哄够, 关于这个问题有一些相关的方面可以继续扩展下:
上面提到的 访问相等 是一个直观的说法, 在大学里学过的编译原理中, 它有更严谨的定义.
2个
dict各自组成的图可以认为是两个自动机, 而1个图中所有的路径就是这个自动机表达的语言. 这个题目的本质也就是判断2个自动机表达的语言是否等价.在有些场合, 这个问题也会表达成判断2个正则表达式是否等价.
关于2个自动机是否等价的比较, 网上直接可以搜到非常成熟的算法.
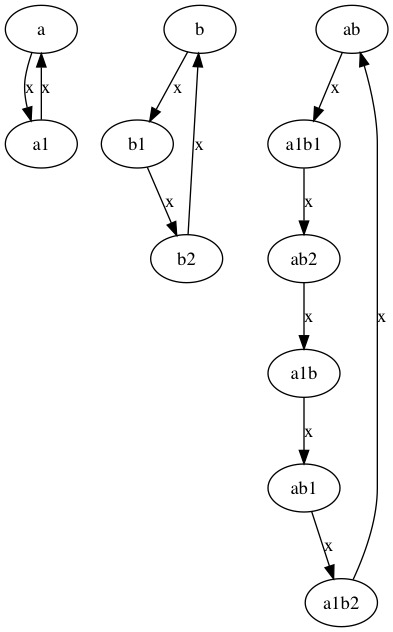
如果把所有路径经过的 节点对 合起来看做1个节点, 那么这个组合的节点对和节点对之间的关联关系会组成一个新的图.
这个新的图是2个图的张量积. 如果2个图是 访问相等 的, 那么他们跟这个新的张量积的图也是 访问相等 的.
而这个问题的解法, 也可以看成对这个张量积图的一次遍历(虽然实际上没有生成这个图).
张量积的图中:
点集是:
a和b的点集的笛卡尔积:{ (a[i], b[j]) }边集的定义:
如果 ai 到 aj 有一条名为k的路径, bk 到 bl 也有一条名为k的路径, 则(ai, bk) 到 (aj, bl) 有一条名为k的路径.
上面2个分支也是有趣话题, 值得深入, 相信对技术人的职业生涯或业余兴趣都会有不少帮助:)