CCF第六次CSP认证考试题解

CCF计算机职业资格认证

CCF*（China Computer Federation）*是计算机领域内一个权威的学术组织，具有高端定位、崇高的价值追求、先进的治理架构和制度规范，拥有众多资深的学者和企业家为骨干会员。CCF开展的该认证工作，具有客观公正及很强的专业性，将解决企业及高校界普遍关心的软件开发人才评价问题，便于有关单位了解求职或求学者的实际开发能力，可有助甄别及吸纳具有真才实学的技术人才，有效地减轻企业与高校在人才选择过程中组织大量上机考核的成本投入。为了更加贴近用人单位的需要，使得该认证有更强的针对性，CCF会同处于行业领先地位的高校与知名企业的专家，共同制定认证标准，审查考题内容。更多详情点我。

CSP认证第六次考试

本次考试时间四小时，共五道题。分别是：

• 数位之和（难度-易）
• 消除类游戏（难度-中）
• 画图（难度-中）
• 送货（难度-难）
• 矩阵（难度-难）

数位之和

题目说明：输入任意一个整数，输出各位数位之和。输入的整数不会超过整型的最大表示范围。 解答：

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNext()) {
            int num = in.nextInt();
            int sum = getSum(num);
            System.out.println(sum);
        }

    }
    public static int getSum(int num) {
        int sum = 0;
        while (num > 0) {
            int temp = num % 10;
            sum += temp;
            num = num / 10;
        }
        return sum;
    }
}

消除类游戏

题目说明： 解答：

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int[][] arrs = null;//原始数组
        int[][] dest = null;//消除之后的数组
        while (in.hasNext()) {
            int row = in.nextInt();
            int col = in.nextInt();
            in.nextLine();
            arrs = new int[row][col];
            dest = new int[row][col];
            for (int i = 0; i < row; i++) {
                for (int j = 0; j < col; j++) {
                    arrs[i][j] = in.nextInt();
                    dest[i][j] = arrs[i][j];
                }
                in.nextLine();
            }
            //处理行
            for (int i = 0; i < row; i++) {
                int start = 0;
                int end = 0;
                for (int j = 0; j < col - 1; j++) {
                    if (arrs[i][j] == arrs[i][j + 1]) {
                        end = j + 1;
                    } else {
                        end = j + 1;
                        if (start == 0) {
                            if (end - start >= 3) {
                                for (int k = start; k < end; k++) {
                                    dest[i][k] = 0;
                                }
                            }
                        } else {
                            if (end - start + 1 >= 3) {
                                for (int k = start; k < end; k++) {
                                    dest[i][k] = 0;
                                }
                            }
                        }
                        start = end;
                    }

                }
                if (start == 0) {
                    if (end - start >= 3) {
                        for (int k = start; k <= end; k++) {
                            dest[i][k] = 0;
                        }
                    }
                } else {
                    if (end - start + 1 >= 3) {
                        for (int k = start; k <= end; k++) {
                            dest[i][k] = 0;
                        }
                    }
                }
            }
            //处理列
            for (int i = 0; i < col; i++) {
                int start = 0;
                int end = 0;
                for (int j = 0; j < row - 1; j++) {
                    if (arrs[j][i] == arrs[j + 1][i]) {
                        end = j + 1;
                    } else {
                        end = j + 1;
                        if (start == 0) {
                            if (end - start >= 3) {
                                for (int k = start; k < end; k++) {
                                    dest[k][i] = 0;
                                }
                            }
                        } else {
                            if (end - start + 1 >= 3) {
                                for (int k = start; k < end; k++) {
                                    dest[k][i] = 0;
                                }
                            }
                        }
                        start = end;
                    }

                }
                if (start == 0) {
                    if (end - start >= 3) {
                        for (int k = start; k <= end; k++) {
                            dest[k][i] = 0;
                        }
                    }
                } else {
                    if (end - start + 1 >= 3) {
                        for (int k = start; k <= end; k++) {
                            dest[k][i] = 0;
                        }
                    }
                }
            }
            for (int[] arr : dest) {
                for (int a : arr) {
                    System.out.print(a + " ");
                }
                System.out.println();
            }
        }

    }
}

画图

题目说明： 解答：

import java.util.Scanner;

public class Main {
    static int COL = 0;
    static int ROW = 0;

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNext()) {
            COL = in.nextInt();
            ROW = in.nextInt();
            int num = in.nextInt();
            String[][] arrs = new String[ROW][COL];

            for (int i = 0; i < arrs.length; i++) {
                for (int j = 0; j < arrs[i].length; j++) {
                    arrs[i][j] = "·";
                }
            }
            in.nextLine();
            for (int i = 0; i < num; i++) {
                int first = in.nextInt();
                if (first == 0) {//表示画线段操作
                    int x1 = in.nextInt();
                    int y1 = in.nextInt();
                    int x2 = in.nextInt();
                    int y2 = in.nextInt();
                    if (x1 == x2) {
                        // |
                        int big = y1 > y2 ? y1 : y2;
                        int small = y1 < y2 ? y1 : y2;
                        for (int start = small; start <= big; start++) {
                            if (arrs[ROW - start - 1][x1] == "-") {
                                arrs[ROW - start - 1][x1] = "+";
                            } else {
                                arrs[ROW - start - 1][x1] = "|";
                            }
                        }
                    }
                    if (y1 == y2) {
                        // -
                        int big = x1 > x2 ? x1 : x2;
                        int small = x1 < x2 ? x1 : x2;
                        for (int start = small; start <= big; start++) {
                            if (arrs[ROW - y1 - 1][start] == "|") {
                                arrs[ROW - y1 - 1][start] = "+";
                            } else {
                                arrs[ROW - y1 - 1][start] = "-";
                            }
                        }

                    }
                } else if (first == 1) {//表示填充操作
                    int x = in.nextInt();
                    int y = in.nextInt();
                    String c = in.next();
                    arrs[ROW - y - 1][x] = c;
                    move(arrs, ROW - y - 1, x, c);
                }
                in.nextLine();
            }
            print(arrs);
        }

    }

    public static void move(String[][] arrs, int row, int col, String c) {
        if (col - 1 >= 0) {
            moveLeft(arrs, row, col, c);
        }
        if (row + 1 < ROW) {
            moveDown(arrs, row, col, c);
        }
        if (col + 1 < COL) {
            moveRight(arrs, row, col, c);
        }
        if (row - 1 >= 0) {
            moveUp(arrs, row, col, c);
        }
    }

    public static void moveLeft(String[][] arrs, int row, int col, String c) {
        col = col - 1;
        if (col >= 0 && arrs[row][col] != "-" && arrs[row][col] != "|"
                && arrs[row][col] != "+" && arrs[row][col] != c) {
            arrs[row][col] = c;
            moveLeft(arrs, row, col, c);
            moveUp(arrs, row, col, c);
            moveDown(arrs, row, col, c);
        }

    }

    public static void moveDown(String[][] arrs, int row, int col, String c) {
        row = row + 1;

        if (row < ROW && arrs[row][col] != "-" && arrs[row][col] != "|"
                && arrs[row][col] != "+" && arrs[row][col] != c) {
            arrs[row][col] = c;
            moveLeft(arrs, row, col, c);
            moveRight(arrs, row, col, c);
            moveDown(arrs, row, col, c);
        }
    }

    public static void moveRight(String[][] arrs, int row, int col, String c) {
        col = col + 1;
        if (col < COL && arrs[row][col] != "-" && arrs[row][col] != "|"
                && arrs[row][col] != "+" && arrs[row][col] != c) {
            arrs[row][col] = c;
            moveRight(arrs, row, col, c);
            moveUp(arrs, row, col, c);
            moveDown(arrs, row, col, c);
        }

    }

    public static void moveUp(String[][] arrs, int row, int col, String c) {
        row = row - 1;
        if (row >= 0 && arrs[row][col] != "-" && arrs[row][col] != "|"
                && arrs[row][col] != "+" && arrs[row][col] != c) {
            arrs[row][col] = c;
            moveUp(arrs, row, col, c);
            moveLeft(arrs, row, col, c);
            moveRight(arrs, row, col, c);
        }

    }

    //打印数组工具函数
    public static void print(String[][] arrs) {
        for (String[] arr : arrs) {
            for (String a : arr) {
                System.out.print(a);
            }
            System.out.println();
        }
    }
}

送货（回忆版）

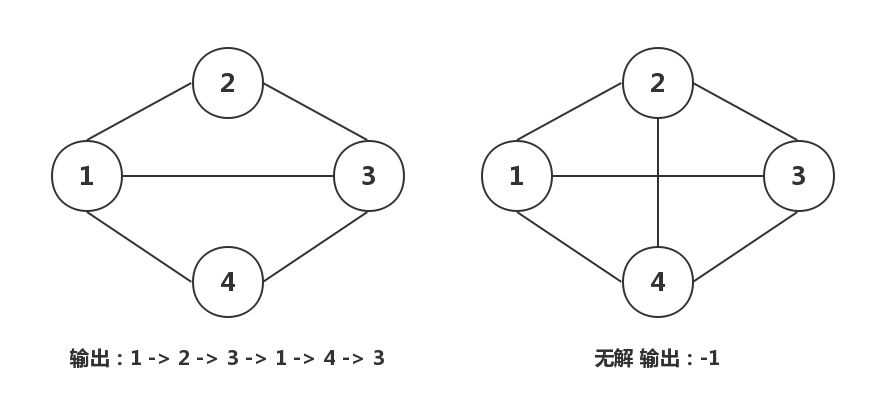
题目说明： 街道是边，圆圈是交叉路口，从路口1出发，一次性遍历所有街道； 如果不存在可以一次性遍历所有街道的路径，则输出 -1； 输入： 路口数m 街道数n N行街道 输出： 如果有多条路径则输出序号依次最小的一条路径，例如demo1存在1,4,3,1,2,3和1,2,3,1,4,3，输出后者 样例输入： 4 5 1 2 1 4 1 3 2 3 3 4 样例输出： 1 2 3 1 4 3 样例输入： 4 6 1 2 1 4 1 3 2 3 3 4 2 4 样例输出： -1 解答：

待补充

矩阵（回忆版）

题目说明： 小明想重新定义世界，初始状态为n维度的列向量b0（注意是列向量，只不过用行方式输入），状态转移矩阵为n维度的方阵A, 向量b1 = A*b0为第一个时刻的状态，bn = A^m*b0为第m时刻的状态，小明据此预测未来；重新定义了向量运算中的求积为逻辑运算与，重定义求和为逻辑运算异或； 其中b0 = A^0*b0 输入： 向量维度n 转移矩阵的第一行（数字间没有空格） …… 转移矩阵的第n行 初始向量 要预测的状态个数m M行预测数字 输出： M个预测状态 样例输入： 3 110 011 111 101 10 0 2 1 7 ……(省略了六个数字) 样例输出： 101 … 110 … (省略了六个输出) 解答： 举例，求1时刻的状态，其实就是使用新的运算法则计算矩阵相乘的结果

┌ 1 1 0 ┐ ┌ 1 ┐   ┌ 1 ┐
| 0 1 1 | | 1 | = | 1 |
└ 1 1 1 ┘ └ 0 ┘   └ 0 ┘

待补充

啥？还有两题？对的，还有俩，不过第四道不会，第五道没写完就自动交卷了。不提也罢，码字速度还要跟上，虽然说机房键盘差劲，也没有我喜爱的IntelliJ，但是要从自身找原因。