一道关于股票最大收益的算法题

前段时间在segmentfault回答了一个关于算法的问题,感觉很有趣,记录下来.

题目是这样的:

给定数组n，包含n天股票的价格price.
一个人一共最多可以买2手股票，但在第一手股票卖出前不能买入第二手股票。如果不买，收益为0.假设每手只买1股。计算这个人最大收益。
输入:[3,8,5,1,7,8]
输出:12

先贴下我的算法代码:

<?php

function getMaxProfilt(array $arr) {
    $len = count($arr);
    $array_tmp = array();
    echo '辅助数组:', '<br />';
    for($i = 0; $i < $len; $i++) {
        for($j = 0; $j < $len; $j++) {
            $array_tmp[$i][$j] = $arr[$j] - $arr[$i];
            echo $array_tmp[$i][$j] . ' ';
        }
        echo '<br />';
    }
    $maxProfit_i = 1;
    $maxProfit_j = 2;
    $maxProfit = $array_tmp[1][2];
    for($i = 1; $i < $len; $i++) {
        for($j = 2; $j < $len; $j++) {
            if($array_tmp[$i][$j] > $maxProfit && $j > $i) {
                $maxProfit = $array_tmp[$i][$j];
                $maxProfit_i = $i;
                $maxProfit_j = $j;
            }
        }
    }
    echo 'maxProfit is :', $maxProfit, '; maxProfit_i is:', $maxProfit_i, '; maxProfit_j is :', $maxProfit_j, '<br />';
    $secondProfit = $array_tmp[0][1];
    $secondProfit_i = 0;
    $secondProfit_j = 1;
    for($i = 0; $i < $maxProfit_i; $i++) {
        //这里控制第二手买入要在第一手卖出的情况下才能买入
        for($j = 1; $j < $maxProfit_i; $j++) {
            if($array_tmp[$i][$j] > $secondProfit && $j > $i) {
                $secondProfit = $array_tmp[$i][$j];
                $secondProfit_i = $i;
                $secondProfit_j = $j;
            }
        }
    }
    echo 'second profit is : ', $secondProfit, '; secondProfit_i is :', $secondProfit_i, '; secondProfit_j is :', $secondProfit_j, '<br />';    
    return $maxProfit + $secondProfit;
}

// $array = [3, 8, 5, 1, 7, 8];
// $array = [1,2,3,4,5,6,7,8];
$array = [2,9,1,9,2,4,8,6,2];

echo getMaxProfilt($array);

以下是思路:

为了方便理解，我画了张图，如下:

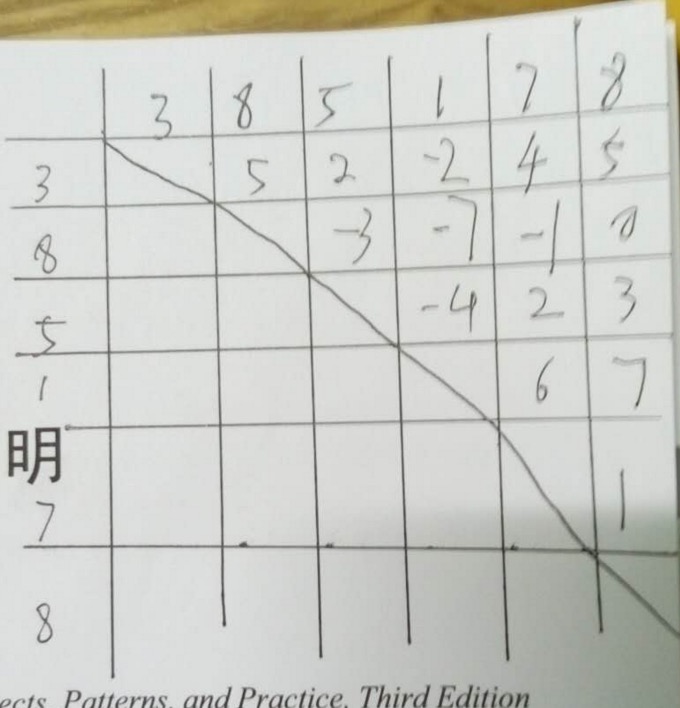
程序思路:

定义参数数组为array;

一开始的想法

一开始我把问题想的很简单，以为只要把两个最大收益相加就行，因为你有一个条 件，第一手没有卖出前不能买入第二手。麻烦的就是这里，所以一开始写代码的时候才发现还是有点复杂。所以用到了二维数组用来控制条件:第二手买入前要卖出第一手;

得到所有可能且有效的收益:

图上能看到二维数组的元素都来自于array后面的数减去其前面的数，而且只有右上方才是真正的收益，假设x轴方向元素下标为j,y轴方向元素下标为i.即有效的收益第一条件为:j>i;

解题关键

有一个很关键的问题要明白，明白这个之后，后面的就好理解了,如下:

有效收益原则

小明在股价3元的时候买入，在第一个8元的时候卖出，得到收益5元，这时候，他就永远不会得到5元后面的收益，即2,-2,4,5。但是能得到5的右下角(不包括5所在的行和列)的收益。我们把这个例子叫做有效收益原则，后面会用到。

很明显图中最大的收益是6和7，但是这违反了有效收益原则。

缩小最大两个有效收益范围

根据有效收益原则逆推，如果我们能确定最大收益的位置，即7的位置，我们就能把两个有效最大收益的范围缩小，一个是7，另一个在7(不包括7的行和列)的左上角。所以我在得到辅助数组后就先找到了7的位置。之所以从－3开始找，是为了排除第一个5是最大收益的情况。

最后的条件

得到了两个最大收益的范围，就差最后一个且最重要的条件了:第二手买入必须在第一手卖出之后。 我还是举例来说明，根据图片我们知道最大收益是7，想要得到7，第一手就必须在股票价格为1的时候卖出第一手股票，然后立即买入。或者股票价格为1的时候第一手股票已经卖出。而7的下标(从0开始)为i=3,j=5.根据有效收益原则，第二大的收益的范围就缩小到i=j=3的左上角了。知道了范围，代码中第三个双重循环就能找到第二大的收益了。

代码讲解:

• 得到有效收益的二维辅助数组(第一个双重循环)
• 得到最大的有效收益及其位置(第二个双重循环)
• 根据上面的位置确定第二大收益的范围
• 根据范围得到第二大收益(第三个双重循环)

整体的过程就是这样了。如果有更好的算法欢迎交流。但是最好用代码交流，因为talk is cheap:-)