原文链接 http://codepub.cn/2015/09/29/2016-campus-recruitment-of-baidu-programming-problem-resolution-software-development/
注:以下为加速网络访问所做的原文缓存,经过重新格式化,可能存在格式方面的问题,或偶有遗漏信息,请以原文为准。
比大小
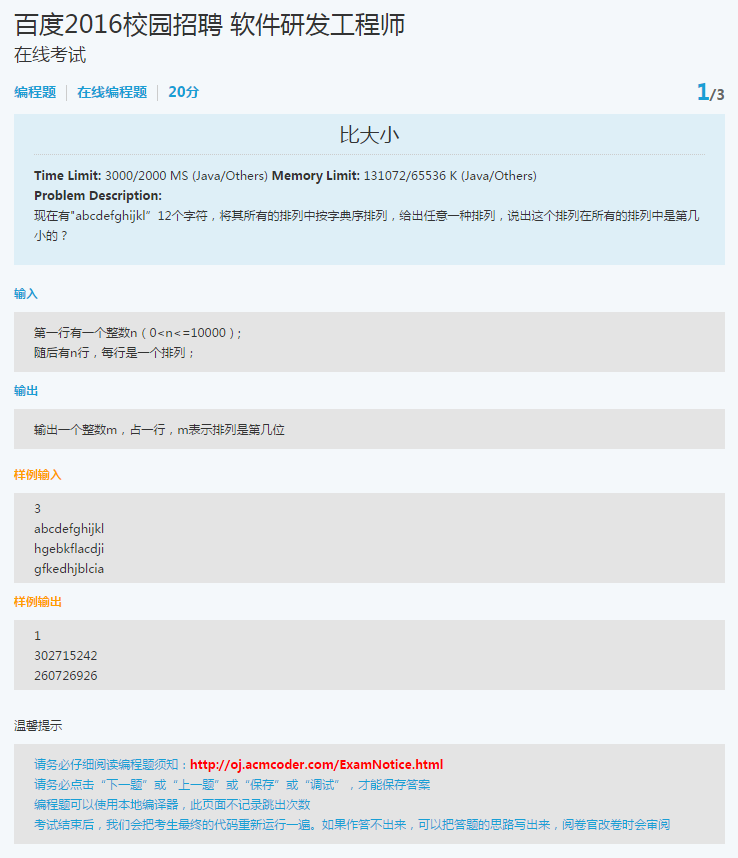
解题思路:解此题需要使用到康托展开,康托展开的公式如下
$$X=a_n*(n-1)!+a_{n-1}*(n-2)!+\cdot\cdot\cdot+a_i*(i-1)!+\cdot\cdot\cdot+a_2*(2-1)!+a_1*(1-1)!$$
公式看不懂没关系,下面以一个例子来讲解公式的使用!
例如:有一个数组S=["a","b","c","d"],它的其中之一个排列是S1=["b","c","d","a"],现在欲把S1映射成X,需要怎么做呢?按如下步骤走起
$$X=a_4*3!+a_3*2!+a_2*1!+a_1*0!$$
- 首先计算n,n等于数组S的长度,n=4
- 再来计算a4="b"这个元素在数组
["b","c","d","a"]中是第几大的元素。"a"是第0大的元素,"b"是第1大的元素,"c"是第2大的元素,"d"是第3大的元素,所以a4=1 - 同样a3="c"这个元素在数组
["c","d","a"]中是第几大的元素。"a"是第0大的元素,"c"是第1大的元素,"d"是第2大的元素,所以a3=1 - a2="d"这个元素在数组
["d","a"]中是第几大的元素。"a"是第0大的元素,"d"是第1大的元素,所以a2=1 - a1="a"这个元素在数组
["a"]中是第几大的元素。"a"是第0大的元素,所以a1=0 - 所以
X(S1)=1\*3!+1\*2!+1\*1!+0\*0!=9 - 注意所有的计算都是按照从0开始的,如果["a","b","c","d"]算为第1个的话,那么将
X(S1)+1即为最后的结果
Java算法实现:
import java.util.Iterator;
import java.util.Scanner;
import java.util.Set;
import java.util.TreeSet;
/**
* <p>
* Created with IntelliJ IDEA. 2015/9/29 16:16
* </p>
* <p>
* ClassName:Main
* </p>
* <p>
* Description:本题需要用到康托展开,其公式为 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0!
* </P>
*
* @author Wang Xu
* @version V1.0.0
* @since V1.0.0
*/
public class Main {
// 3
// abcdefghijkl
// hgebkflacdji
// gfkedhjblcia
static int charLength = 12;//定义字符序列的长度
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
String lines[] = new String[n];
int res[] = new int[n];//存储结果的数组
for (int i = 0; i < n; i++) {
lines[i] = scanner.next();
res[i] = calculate(lines[i]);
}
for (int s : res) {
System.out.println(s);
}
}
}
//计算某个字符序列的位次
private static int calculate(String line) {
Set<Character> s = new TreeSet<Character>();
for (char c : line.toCharArray()) {
s.add(c);
}
//存储每一个字符在该序列中是第几大的元素,然后将其值存储到counts数组中
int counts[] = new int[s.size()];
char[] chars = line.toCharArray();
for (int i = 0; i < chars.length; i++) {
Iterator<Character> iterator = s.iterator();
int temp = 0;
Character next;
while (iterator.hasNext()) {
next = iterator.next();
if (next == chars[i]) {
counts[i] = temp;
s.remove(next);
break;
} else {
temp++;
}
}
}
int sum = 1;
for (int i = 0; i < counts.length; i++) {
sum = sum + counts[i] * factorial(charLength - i - 1);
}
return sum;
}
//计算阶乘的函数
private static int factorial(int n) {
if (n > 1) {
return n * factorial(n - 1);
} else {
return 1;
}
}
}
拓展一下-求其逆过程

解题思路:使用康托逆展开,辗转相除得到的值为这个字符是第几大,这样取出对应位置的字符,然后利用后面的字符覆盖该字符即可,防止取到重复的字符。取模得到余数之后,重复上述过程。
例如:已知S=["a","b","c","d"],那么当输入10的时候,或者说X(S1)=9的时候能否推出S1=["b","c","d","a"]呢?
由
$$X(S1)=a_4*3!+a_3*2!+a_2*1!+a_1*0!=9$$
所以问题变成由9能否唯一地映射出一组a4、a3、a2、a1?首先如果不考虑ai的范围,那么有如下:
$$1*3!+1*2!+1*1!+0*0!=9$$
$$0*3!+4*2!+1*1!+0*0!=9$$
$$0*3!+3*2!+3*1!+0*0!=9$$
$$0*3!+2*2!+5*1!+0*0!=9$$
......,但是每一个ai其实是有取值范围的,首先要知道ai表示的含义,其代表在当前剩余的序列中ai是处于第几大的位置,那么满足0<=ai<=i,同时a1必然为0,因为最后始终剩余一个元素。所以上式中只有第一个满足条件,那么a4=1,a3=1,a2=1,a1=1。推导出S1=["b","c","d","a"]。
Java算法实现:
import java.util.Scanner;
/**
* <p>
* Created with IntelliJ IDEA. 2015/9/29 16:16
* </p>
* <p>
* ClassName:Main
* </p>
* <p>
* Description:本题需要用到康托展开,其公式为 X=an*(n-1)!+an-1*(n-2)!+...+ai*(i-1)!+...+a2*1!+a1*0!
* </P>
*
* @author Wang Xu
* @version V1.0.0
* @since V1.0.0
*/
public class MainExpand {
static int charLength = 12;//定义字符序列的长度
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
while (scanner.hasNextInt()) {
int n = scanner.nextInt();
int lines[] = new int[n];
String res[] = new String[n];//存储结果的数组
for (int i = 0; i < n; i++) {
lines[i] = scanner.nextInt();
res[i] = calculate(lines[i] - 1);
}
for (String s : res) {
System.out.println(s);
}
}
}
//计算某个字符序列的位次
private static String calculate(int line) {
char alpha[] = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l'};
StringBuilder sb = new StringBuilder();
for (int i = charLength - 1; i >= 0; i--) {
int temp = line / factorial(i);
line = line % factorial(i);
sb.append(String.valueOf(alpha[temp]));
for (int j = temp; j < alpha.length - 1; j++) {
alpha[j] = alpha[j + 1];
}
}
return sb.toString();
}
//计算阶乘的函数
private static int factorial(int n) {
if (n > 1) {
return n * factorial(n - 1);
} else {
return 1;
}
}
}
判断字符串是否出现
 解题思路:
解题思路:
- 将字符串a存储在一个map集合中,以每个字符的ASCII码作为key,以其出现的次数作为value,记为aMap
- 遍历字符串b,对于b中的每一个字符,如果aMap的key中含有该字符的ASCII码,如果该key对应的value>1,那么将value值减1
- 否则value=1的话,那么将该键值对从aMap中移除
- 在判断aMap的key是否包含b中的某个字符的时候,只要有一次不包含,那么就说明没有都出现
- 否则的话,表示b中的字符在a中都出现过
Java算法实现:
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
/**
* <p>
* Created with IntelliJ IDEA. 2015/9/28 20:05
* </p>
* <p>
* ClassName:test
* </p>
* <p>
* Description:TODO
* </P>
*
* @author Wang Xu
* @version V1.0.0
* @since V1.0.0
*/
public class Main {
public static void main(String[] args) {
//以某个字符的ASCII码作为key,以其出现的次数作为value
Map<Integer, Integer> aMap = new HashMap<Integer, Integer>();
Scanner input = new Scanner(System.in);
while (input.hasNextLine()) {
String a = input.nextLine();
String b = input.nextLine();
char[] chars = a.toCharArray();
for (char c : chars) {
if (aMap.keySet().contains((int) c)) {
int temp = aMap.get((int) c);
aMap.put((int) c, (temp + 1));
} else {
aMap.put((int) c, 1);
}
}
char[] chars1 = b.toCharArray();
boolean flag = true;
for (char c : chars1) {
if (aMap.keySet().contains((int) c)) {
int temp = aMap.get((int) c);
if (temp == 1) {
//说明只有一个
aMap.remove((int) c);
} else {
//说明多过于一个
aMap.put((int) c, (temp - 1));
}
} else {
flag = false;
break;
}
}
if (flag) {
System.out.println(1);
} else {
System.out.println(0);
}
aMap.clear();
}
}
}
组合概率
 解题思路:
需要递推公式,然后用动态规划求解。
解题思路:
需要递推公式,然后用动态规划求解。
Java算法实现:
import java.text.DecimalFormat;
import java.util.Scanner;
/**
* <p>
* Created with IntelliJ IDEA. 2015/9/28 20:30
* </p>
* <p>
* ClassName:Test3
* </p>
* <p>
* Description:动态规划求解
* </P>
*
* @author Wang Xu
* @version V1.0.0
* @since V1.0.0
*/
public class Main3 {
static DecimalFormat dec = new DecimalFormat("0.0000");
static double v[][];//表示取i个数时和为j的概率
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
while (input.hasNextInt()) {
int n = input.nextInt();
int a = input.nextInt();
int b = input.nextInt();
int x = input.nextInt();
v = new double[n + 1][x + 1];
double sum = b - a + 1;
for (int i = a; i <= b; i++) {
v[1][i] = 1.0 / sum;//取1个数和为i的概率
}
for (int i = 1; i <= n; i++) {//对n个数进行迭代
for (int j = a; j <= b; j++) {//
for (int k = 1; k <= x; k++) {
if (k >= j) {
// print(v);
// System.out.println();
v[i][k] = v[i][k] + v[i - 1][k - j] / sum;
}
}
}
}
//输出取n个数和为x的概率
System.out.println(dec.format(v[n][x]));
}
}
private static void print(double[][] v) {
for (int i = 0; i < v.length; i++) {
for (int j = 0; j < v[i].length; j++) {
System.out.print(v[i][j] + "\t");
}
System.out.println();
}
}
}
参考文献 [1] http://www.jeepshoe.org/416642954.htm [2] http://www.cnblogs.com/sunus/p/4536082.html
算法如有疏漏或不妥之处,还望不吝赐教!